DSP
Un signal est la description de l'evolution d'un phenomene physique.
Ce que nous apprend le paradoxe de Zenon est le fait que si on admet qu'une fleche doit parcourir une distance d en un temps t, alors si on divise cette distance par deux, la fleche devra passer par ce point.
Mais si on divise a nouveau cette distance par deux, on s'apercoit que la fleche devra aussi passer par ce point.
On peut des lors en conclure que pour aller d'un point A a un point B, la fleche devra passer par une infinite de points.
Et que si elle doit accorder du temps a chaque point, elle ne devrait jamais arriver au point B, car le temps deviendrait infini.
Ceci peut etre toutefois mis en equation et resolu par la formule suivante : $$\sum_{n=1}^{+\infty}\frac{1}{2^{n}}=1$$
Voyons maintenant la formule qui permet de calculer la moyenne d'un signal continu : $$\bar{x}=\frac{1}{b-a}\int_{a}^bf(t)dt$$
Il s'agit de l'aire sous la courbe, element classique des integrales et permet ainsi de calculer la moyenne de ce signal (par exemple la temperature).
Et enfin la moyenne des valeurs discretes : $$\bar{x}=\frac{1}{N}\sum_{n=0}^{N-1}x[n]$$
Le theoreme d'echantillonnage
Cette theorie nous vient de Nquist et Shannon dans les annees 20.
Avec ce theoreme on va ajouter, a chaque valeur discrete ($x[n]$), un schema particulier.
Voici sa formule : $$ x(t) = \sum_{n=-\infty}^{+\infty}x[n]\frac{\frac{sin(\pi(t-nT_s)}{T_s}}{\frac{\pi(t-nT_s)}{T_s}} $$
Une petite precision ici, le terme $x(t)$ est une fonction continue.
Alors que $x[t]$ est un echantillon, donc une valeur discrete.
Nous en avons une troisieme qui est $\hat{x}[t]$ et permet de dire que nous avons ici un certain niveau de valeurs possible en amplitudes (voir ADC avec 16 ou 32 bits par exemple).
De sorte qu'en ajoutant chaque fonction, obtenue a partir de chaque valeur discrete, on va pouvoir retrouver la fonction originale.
En fait on va diviser la fonction originale en plusieurs valeurs discrete, avec lesquelles on va pouvoir obtenir la fonction de depart, en les ajoutant.
La seule chose qui permet a cette technique d'etre vrai est que la fonction de depart ne doit pas etre trop rapide, c'est a dire ne contenant pas trop de frequences hautes.
On appelle cela des fonctions sinc, donc voici une representation graphique :
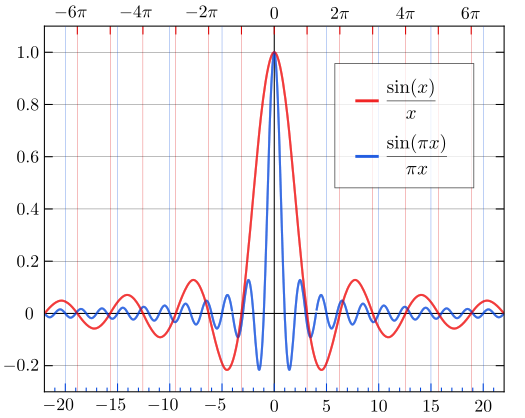
Ou encore :
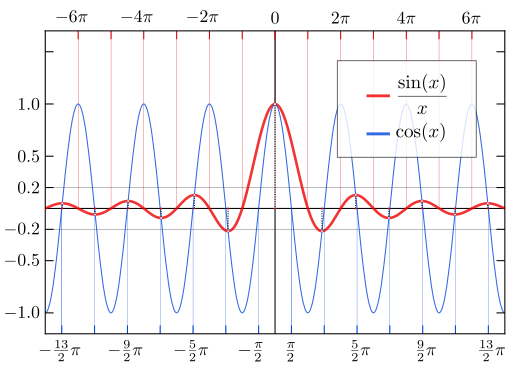
Le bruit
Il est introduit apres chaque digitalisation, c'est a dire transformation d'un phenomene analogique en numerique.
De sorte que pour produire un signal numerique il faut attenuer le signal analogique et y ajouter du bruit.
En faisant ca il est necessaire d'introduire du gain pour retrouver le signal du depart.
Mais forcement en amplifiant le signal numerique on va aussi amplifier le bruit introduit precedemment.
La formule est : $$ \hat{x}_1(t) = G[\frac{x(t)}{G}+\sigma(t)] = x(t) + G\sigma(t) $$
Ou $\sigma(t)$ est le bruit et $G$, le gain.
C'est exactement ce qu'on a lorsqu'on effectue une copie d'une copie.
On doit alors s'accomoder du bruit qui est de fait de plus en plus present lorsqu'on fait des copies de copies.
On dit que le signal est corrompu par le bruit.
Pour retirer ce bruit et retrouver le signal d'origine, il va falloir utiliser ce que l'on appelle un operateur threshold, ou tout simplement threshold.
Il va permettre de dire que si le signal corrompu est en dessous de 0 volt, on va admettre que le signal est -5 V et s'il est au dessus de 0 V, alors on a +5 V.
De sorte qu'on soit sur que l'on a bien soit 0 soit 1.
Pour les signaux non periodiques
Energie
L'energie est la somme des carres des echantillons, que l'on peut formuler ainsi : $$ E_x = \sum_{n=-\infty}^{+\infty}|x[n]|^2 $$
Puissance
La puissance reprend l'equation de l'energie et fait entrer dans la formule la longueur de la fenetre de tir ($N$). $$ P_x = \lim_{N\to +\infty} \frac{1}{2N+1} \sum_{n=-N}^{+N} |x[n]|^2 $$
C'est un peu comme l'energie instanee de la sequence.
Pour les signaux periodiques
Energie
Ici l'energie est infinie : $$ E_{\bar{x}}=+\infty $$
Puissance
Et la puissance peut se resumer ainsi : $$ P_{\bar{x}}= \frac{1}{N} \sum_{n=0}^{N-1} |\bar{x}[n]|^2 $$
Nous avons donc une sequence finie alors meme que l'energie est, elle, infinie.
Les signaux
Un signal transporte de l'information. C'est cette information que l'on va chercher a apprehender au travers de differentes techniques pour que l'on puisse la mesurer et la comparer a d'autres mesures. De sorte que le signal processing va manipuler l'information transporte par les signaux. Les valeurs n prisent dans le signal x[n] sont des entiers dits aussi integers. On dit que ce sont des variables independantes. Et le signal est une fonction qui caracterise une variable independante en une variable dependante. Une variable dependante est un nombre real ou complexe.
Difference entre infinite-length discrete time signals and finite-length DTS. Finite is from a range. For example for n = 0 to n = 80. En dehors de cette limite, la fonction est indefinie. Dans les formules quand on voit N cela veut dire periode.
Donc que le signal est periodique. Ex: $$x[n+mN] = x[n]$$ Avec scilab on fait : clf(1) h=scf(1) t=linspace(0, 10*%pi, 10) y=sin(t) plot2d3(t,y) title('Lol') ylabel('Amplitude') xlabel('Echantillon') plot(t,y,'m') Le fait de passer d'un infinite length signal to a finite s'appelle le windowing. En gros le fenetrage, on prend une fenetre du temps. L'inverse, passage d'un temps fini a infini se fait par (infinite) zero padding ou par periodization. Un signal de longueur infini sur une ligne infinie. Un signal periodique s'articule autour d'un cercle. Une horloge avec N heures. Un signal causal est un signal ou toutes les valeurs de x[n] sont egales a 0 si n<0. Donc pour les valeurs negatives. Un signal anticausal est l'inverse, toutes les temps de valeurs positives et aussi 0 sont egales a 0. Un signal pair est symetrique par rapport a 0. Le temps -5 a la meme valeur que 5. Un signal impair est aussi symetrique, comme un mirror. Sauf que on doit changer le signe de la valeur, par exemple la valeur de -5 = 5 avec le signe inverse --> -5 = -(5). Ceci a son importance car chaque signal peut etre decompose en la somme des ces parties paires et impaires.
On peut le voir :
Partie even : $ e[n]= \frac{1}{2}(x[n] + x[-n]) $
Partie odd : $ o[n]= \frac{1}{2}(x[n] - x[-n]) $
Au final : $ x[n] = e[n] + o[n] $ $$ x[n] = \frac{1}{2}(x[n] + x[-n]) + \frac{1}{2}(x[n] - x[-n]) $$ $$ x[n] = \frac{1}{2}(x[n] + x[-n] + x[n] - x[-n]) $$ $$ x[n] = \frac{1}{2}(2x[n]) = x[n] $$
Les signaux digitaux sont des sous classes des signaux a temps discrets.
La difference est qu'ici notre variable independante n ne va pas appartenir a $\mathbb{R}$ mais a $\mathbb{Z}$, donc uniquement des entiers.
Ceci va evidemment faciliter grandement les choses lorsque nous allons allouer pour chaque valeur 1, 2, 3, 4, etc. des nombres binaires qui ne comprennent que des entiers et donc aucune virgule.
Il est egalement judicieux de faire la difference entre un signal discret et un signal continu. En voici un exemple :

clf(1);
// 1
h=scf(1);
x=0:1:10;
y=ones(1,11); // puts 1 as amplitude in each time value
subplot(2,1,1); // height divised by, width divided by, diagram number
plot2d3(x,y); // 1st diagram, displays vertical lines.
plot(x,y, 'b.') // displays blue dots on above each vertical line
xlabel('Time');
ylabel('Amplitude');
title('Discrete Signal');
subplot(2,1,2);
plot(x,y); // 2nd diagram
xlabel('Time');
ylabel('Amplitude');
title('Continuous Signal');
The delta function
Cette fonction est sans doute la plus simple des signaux.
Si n = 0 $$ \delta[n]=1 $$
Sinon $$ \delta[n]=0 $$
On la formalise par :
On peut aussi shifter cette fonction. Par exemple si on a m = 5, on aura donc : $$ \delta[n-m]=\delta[n-5] $$
m est une constante.
Donc $x[m] est egalement une constante et non un signal.
On va utiliser $\delta[n]$ pour multiplier un signal $x[n]$ comme ceci : $$ y[n]=x[m]\delta[n-m] $$
Ainsi avec m = 5, on a : $$ y[n]=x[5]\delta[n-5] $$
The unit step
Ce signal peut etre defni par le fait que $u[n] = 0$ si n est inferieur a 0.
Dans toutes les autres cas, on a $u[n] = 1$.
On peut egalement shifter ce signal de 4 : $$ u[n-m]=u[n-4] $$
Du coup le signal ne vaudra 1 qu'a partir de n = 4.
Ce qui alors nous permettre de multiplier le signal de depart par le unit step pour ne recuperer qu'une partie du signal d'origine, celle qui matche avec le step unit.
On a ici la meme chose qu'avec un & en operation binaire. $$ y[n]=x[n]u[n-m] $$
Ainsi avec m = 4, on a : $$ y[n]=x[n]u[n-4] $$
The unit pulse
Le signal $p[n]$ vaudra 1 entre 2 n dans le temps, par exemple N1 et N2.
Tout le reste du temps cela vaudra 0.
Ce qu'on peut representer de facon un peu compliquee par : $$ p[n] = u[n-N1]-u[n-(N2+1)] $$
The real exponential
Derriere ce nom ce cache une notion assez simple.
Le reel est un nombre reel, donc defini sur $\mathbb{R}$. Donc tous les nombres de l'Univers (rien que ca).
L'exponentielle est tout simplement une fonction qui prend en exposant un nombre pris sur l'ensemble $\mathbb{R}$.
On peut resumer cela avec la formule suivante : $$ r[n] = a^{n} $$
Ou $r$ = la fonction, $a$ est la valeur constante, $n$ est la valeur dans le temps.
Donc si 0 < a < 1, la fonction diminue jusqu'a atteindre 0 (infini).
Si a > 1, la fonction evolue dans le temps vers l'infini positif.
Aliasing of sinusoids
Prenons deux sinusoides avec deux frequences differentes : $$ x_1[n] = e^{j(\omega n + \phi)} $$ $$ x_2[n] = e^{j((\omega + 2\pi) n + \phi)} $$
Cependant si on fait : $$ x_2[n] = e^{j((\omega + 2\pi) n + \phi)} = e^{j(\omega n + \phi) + j2\phi n} = e^{j(\omega n + \phi)} e^{j2\phi n} = e^{j(\omega n + \phi)} = x_1[n] $$
Dans la formule ci-dessus, $e^{j2\phi n}$ est toujours egal a 1.
Ce qui fait que $x_1$ et $x_2$ sont identiques alors meme qu'ils ont des frequences differentes !
Ainsi $x_1$ et $x_2$ sont des alias, et ce phenomene s'appelle l'aliasing.
Ceci fonctionne avec tous les multiples de $2\pi$.
Generalement deux intervales sont utilises en traitement du signal : $$ 0 \le \omega \lt 2\pi $$ $$ -\pi \lt \omega \le \pi $$
On voit toutefois que la distance entre les deux extrimites est egales a $2\pi$.
Low and high frequencies
On remarque que lorsque la frequence est lente, on a $\omega$ qui est proche de $0$ ou $2\pi$ rad, comme ici avec $-sin(\frac{\pi}{10}*n)$ :

Alors que lorsque la frequence est rapide, on a $\omega$ qui est proche de $-\pi$ ou $-\pi$ rad, comme ici avec $-sin(\frac{9\pi}{10}*n)$ :

Dont voici le code Scilab :
clf(1); clf(2); h=scf(1); n=0:1:30 x = -sin((%pi/10)*n); plot2d3(n, x); plot(n,x,'.') h=scf(2); n=0:1:30 x = -sin((9*%pi/10)*n); plot2d3(n, x); plot(n,x,'.')
Sur le second schema on voit qu'on a un coup une valeur positive et un coup une valeur negative.
Ceci est du au fait que la frequence est tellement elevee qu'on n'intercepte pas assez de donnees pour les afficher toutes. Ce qui donne cette impression d'avoir deux sinusoides si on regarde globalement le schema.
Periodicity of sinusoids
Admettons une frequence $\omega = \frac{2 \pi k}{N}$ et une sinusoide definit par $x_1[n] = e^{j((\omega n + \phi)}$, on peut ainsi avoir : $$ x_1[n + N] = e^{j((\omega (n + N) + \phi)} = e^{j(\omega n + \omega N + \phi)} = e^{j(\omega n + \phi)} e^{j (\omega N)} = e^{j(\omega n + \phi)} e^{j (\frac{2 \pi k}{N} N)} = x_1[n] $$

En conclusion, on peut voir que $x_1[n]$ est periodique, dans notre cas nous avons $N=16$ donc de periode 16.
Toutes les 16 valeurs de n, on retrouve exactement la meme valeur comprise entre $-1$ et $1$.
La frequence $\omega = \frac{2 \pi k}{N}$ est ce qu'on appelle un harmonique.
En effet, $2 \pi$ est finalement divise par $\frac{k}{N}$ car $2 \pi$ est un tour complet autour du cercle trigonometrique.
N'oublions pas que $k$ et $N \in \mathbb{Z}$.
Les sinusoides non periodiques
Pour cela il suffit quela frequence $\omega \ne \frac{2 \pi k}{N}$.
On voit alors que $x_2[n + N] \ne x_1[n]$ et que donc cette sinusoide n'est pas periodique : $$ x_2[n + N] = e^{j((\omega (n + N) + \phi)} = e^{j(\omega n + \omega N + \phi)} = e^{j(\omega n + \phi)} e^{j (\omega N)} \ne x_1[n] $$

h=scf(4); n=0:1:48 x = -sin((%pi)*n); plot2d3(n, x); plot(n,x,'.')
La sinusoide oscille bien entre un minimum et un maximum mais on voit tres bien qu'elle n'est pas periodique.
Par consequent $\omega$ n'est pas harmonique.
On en conclut donc que seules les sinusoides periodiques ont une frequence harmonique.
C'est a dire dans la sinusoide $e^{j(\omega n + \phi)}$ on a une frequence $\omega = \frac{2 \pi k}{N}$.
Vector space
Un espace vectoriel $V$ est une collection de vecteurs tels que si $x, y \in V$ et $\alpha$ est un scalaire, alors : $$ \alpha x \in V $$ $$ x+y \in V $$
On sait que $\alpha \in \mathbb{R}$ ou $\mathbb{C}$.
Les vecteurs sont ainsi fort utiles en signal processing dans la mesure ou en dilatant (scaling) $\alpha x$ on va en fait amplifier ou attenuer le signal par ce facteur $\alpha$.
En ajoutant $x$ et $y$ on va creer un nouveau signal qui mixe $x$ et $y$.
Multiplication d'un signal par un scalaire
Dans cet exemple nous allons prendre une sinusoide classique puis appliquer. a chaque sample, une multiplication par lui-meme, et ce 9 fois. Pour etre plus clair on va mettre la valeur de l'echantillon a l'exposant 9.
Ici le scalaire est bien entendu le chiffre 9.
Sur le 3e graphique on va appliquer une racine cubique representait par un exposant a $y1$ de la forme : $y^{(\frac{1}{3})}$

disp("------------ BEGIN -----------");
clf(1);
// all
h=scf(1);
n=3;
axis_x = "x";
axis_y = "y";
// 1
subplot(n,1,1); // height divised by, width divided by, diagram number
x=0:0.1:20; // from 0 to 20 with 0.1 of gap between each x
y1=sin(x); // takes each x and adds it to the y axis
plot2d3(x,y1); // displays vertical black lines
plot(x,y1) // draws the blue curve that links each vertical lines
xtitle("y1 = sin(x)", axis_x, axis_y); // title
// 2
subplot(n,1,2);
y2=y1.^9;
plot2d3(x,y2);
plot(x,y2)
xtitle("y2 = y1^9", axis_x, axis_y);
// 3
subplot(n,1,3);
y3=y1.^(1/3);
plot2d3(x,y3);
plot(x,y3)
xtitle("y3 = y1.^(1/3)", axis_x, axis_y);
disp("------------ END -----------");
Adding, substracting signals
Ici on va ajouter a un signal de base, une sinusoide. On va ensuite soustraire la sinusoide au signal de depart. Enfin on ajoutera les nouveaux signaux entre eux et on divisera le tout par deux. On retrouvera alors le signal de depart.
Ainsi dans l'image ci-dessous, on a :
- $y1=x$
- $y2=sin(x)^2$
- $y3=y1+y2$
- $y4=y1-y2$
- $y5=\frac{(y3+y4)}{2}$

disp("------------ BEGIN -----------");
clf(1);
// all
h=scf(1);
n=5;
axis_x = "x";
axis_y = "y";
// 1
subplot(n,1,1); // height divised by, width divided by, diagram number
x=0:0.1:20; // from 0 to 20 with 0.1 of gap between each x
y1=(x); // takes each x and adds it to the y axis
plot2d3(x,y1); // displays vertical black lines
plot(x,y1) // draws the blue curve that links each vertical lines
xtitle("y1 = x", axis_x, axis_y); // title
// 2
subplot(n,1,2);
y2=sin(x).^(2);
plot2d3(x,y2);
plot(x,y2)
xtitle("y2 = sin(x)", axis_x, axis_y);
// 3
subplot(n,1,3);
y3=y1+y2;
plot2d3(x,y3);
plot(x,y3)
xtitle("y3 = y1 + y2", axis_x, axis_y);
// 4
subplot(n,1,4);
y4=y1-y2;
plot2d3(x,y4);
plot(x,y4)
xtitle("y4 = y1 - y2", axis_x, axis_y);
// 5
subplot(n,1,5);
y5=(y3+y4)/2;
plot2d3(x,y5);
plot(x,y5)
xtitle("y5 = (y3 + y4) / 2", axis_x, axis_y);
disp("------------ END -----------");
Transpose of a vector
Il s'agit de la conversion d'une colonne en ligne ou d'une ligne en une colonne.
Il existe egalement la conjugate transpose (aussi connu sous le nom de la transposee de Hermite, ou dite hermitienne.
The inner product
On parle aussi de dot product.
Cet inner product prend deux signaux, etant des vecteurs sur $\mathbb{C}^{N}$), et produit un unique nombre complexe.
$N$ represente le nombre de dimensions.
La formule est la suivante : $$ \langle x, y \rangle = y^{H} x = \sum\limits_{n=0}^{N-1}x[n]y[n]^* $$
Ainsi l'expression $\langle x, y \rangle$ se lit : l'inner product entre x et y.
De meme, $y^{H} x$ se lit $y$ hermitien fois $x$. Il s'agit ici de prendre la ligne representee par $y^{H}$ et de la multiplie par la colonne representee par $x$.
On abouti alors a un seul nombre, etant par ailleurs complexe. Ceci est la representation de cette formule : $$ \sum\limits_{n=0}^{N-1}x[n]y[n]^* $$
On a ensuite la formule de l'angle entre le vecteur $x$ et le vecteur $y$, definit sur $\mathbb{R}^{N}$ : $$ cos\theta_{x,y} = \frac{\langle x, y \rangle}{||x||_2||y||_2} $$
Sachant que $||x||_2||y||_2$ est la norme 2 de x et norme 2 de y.
On a aussi la meme formule mais definit sur $\mathbb{C}^{N}$ : $$ cos\theta_{x,y} = \frac{Re\{\langle x, y \rangle\}}{||x||_2||y||_2} $$
Prenons un exemple sur $\mathbb{R}^{2}$ avec $$ x = \begin{bmatrix} 1 \cr 2 \end{bmatrix} et \; y = \begin{bmatrix} 3 \cr 2 \end{bmatrix} $$
Pour le numerateur on aura donc $$ 1*3 + 2*2 = 7 $$
et pour le numerateur cela sera $$ ||x||_2^2=1^2+2^2=5 \; et \; ||y||_2^2=3^2+2^2=13 $$
Donc : $$ \theta_{x,y} = arcos \left( \frac{7}{\sqrt{5} \sqrt{13}} \right)= arcos \left( \frac{7}{\sqrt{65}} \right) = 0.519 \; rad = 29.7^{\circ} $$
Orthogonal vectors
Deux vecteurs sont dits ortogonaux si leur inner product est egal a 0 : $$ \langle x,y \rangle = 0 $$
Ceci nous amene a en deduire que donc : $$ \theta_{x,y} = \pi \, rad = 90^{\circ} $$
Cauchy-Scharwz inequality
Ce theoreme nous apprend que si $|\langle x,y \rangle|$ est proche de $0$, alors les deux signaux $x$ et $y$ sont differents.
Et si $|\langle x,y \rangle|$ est proche de $||x||_2||y||_2$, alors les deux signaux sont similaires.
Par exemple si on souhaite reconnaitre une personne d'apres une image, on va lancer la recherche dans la base de donnees.
Le resultat sera celui qui aura l'inner product le plus grand. Donc le plus loins de 0 et le plus proche de la norme 2 de x et de y.
Sachant que ce dernier est proche de 1 car : $$ 0 \le \left\lvert\frac{\langle x, y \rangle}{ \|x\|_2\|y\|_2 }\right\rvert \le 1 $$
En effet ceci equivaut a : $$ 0 \le | \langle x, y \rangle | \le \|x\|_2\|y\|_2 $$